学習と姿勢に何が関係あるのだろうと思ったこともあるかもしれませんが学習と姿勢はとても深い関係があります。

結論から言うと集中力と集中できる時間が変わります。どういうことかというと、姿勢がよくないと腰が曲がり、呼吸が浅くなります。その結果ぼーっとするようになります。

ぼーっとする。つまり、集中していない状態になってしまいます。

皆さんもわかっているように集中せず学習していると学習していることが身に付く事はありません。

やはり、ティエラの教室に通い、一生懸命頑張ろう！と思っている皆さんには学習する全ての瞬間を大切にさせたいと考えています。

一生懸命頑張ろうと思っている君達だからこそ、姿勢を正し、一生懸命頑張らせたいです。

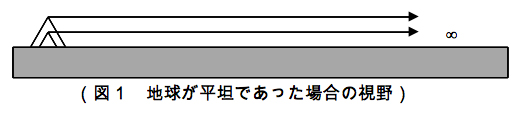
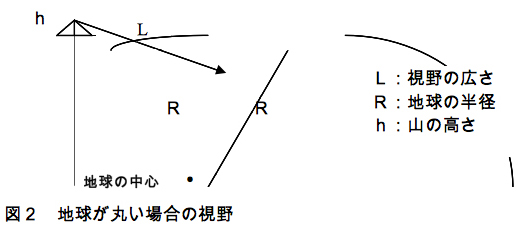
想像してみてほしい。
目の前に小学２年生の子がいる。この子はなかなか九九が覚えられず悩んでいる。数日後にはクラスの前に立って九九の暗唱を発表しなければならない。
さあ、君たちならば、この子になんて声をかけてあげるか。

君たちの中には、小学校に通う前から家庭の中で九九を練習させられて、いざ小学校で九九を習うころには、九九がある程度言えるようになっていた子も少なくないかもしれない。
でも、君たちはもう忘れてしまったかもしれないが、小２算数の最大の山場である九九を覚えるのは大変なんだ。
小２の子を抱える家庭では、家族中を巻き込んで大騒ぎになることもよくある。

そんな、なかなか九九が覚えられない小２の子がいる保護者をターゲットにした便利ツールもたくさん販売されている。

さて、なかなか九九が覚えられない子を、君たちはどうやって助けてあげるか。

「九九のうた」というＣＤを買って聞かせてあげるか？　九九のゲームソフトを買ってあげるか？　それともその子の横について、１×１＝１　から　９×９＝８１　まで、一つ一丁寧に教えてあげるか？

そんなことはしないよね？

答えは明白。声に出して繰り返し練習させるのが最善策。何度も何度もひたむきに練習させればできるようになる。

「もっと楽に覚えたいなぁ」「もっと楽しく教えてよ」「九九の練習は面倒だなぁ」「九九の練習なんかやりたくないよ」「ぼくのやる気を出させてよ」と言ってきたら、どうする？

「文句を言わずに何度も練習しなさい！」と言ってあげれば良いよね。

では、最後にもう一度想像しよう。

目の前になかなか成績が上がらず、目標とする結果が出せずに悩んでいる子がいる。そう、君たち自身だ。

君たちは、君たち自身になんて声をかける？

あなたは社会が好きですか？
多くの歴史嫌いの人が口をそろえて「覚えられない」「歴史の流れが分からない」
と言います。なぜそうなるのか。
答えは簡単です。意味もなく丸覚えをしようとした結果、頭の中で知識がバラバラに散らばっているからです。確かに覚えないといけない部分はあります。しかし意味のないものを記憶に残すことは困難です。さまざまな出来事を網の目のように結ぶことで脳に定着していきます。

例えば平安時代で学習した、「摂関政治」「院政」「平清盛」をストーリー化して説明できますか？なぜ藤原氏のあとに院が政治の実権を握ることができ、その後の平清盛が権勢を誇ったのか。当時の権力者の気持ちになって参考書を読めば、驚くほど理解しやすくなるはずです。完全に「暗記」と思われている各時代の文化にしても同様です。文化の政治的背景を理解すれば、その文化の美術や文学がなぜそのようなものになったかが納得して覚えられるようになるでしょう。試しに参考書「くわしい歴史」の文化の特徴と、その時代の政治を照らし合わせてみてください。

大切なのは「理由」を考えることです。そして出来事などの知識を「理由」で結び合わせていくことです。その最初の知識を持つために「暗記」するといったイメージです。
覚えた出来事などを「点」とすれば、その「点」と「点」を出来事の理由を通じてつなぎ「線」で結ぶ。歴史の得意な人はその「点」のつなぎをストーリー化するのが上手な人ですね。

各時代に登場する「権力者」を軸に歴史の流れを整理してみると分かりやすいかもしれません。みなさんも一度やってみてください。

今週は先生が大学に入学してから間もない頃の話です。
今でも鮮明に覚えているのは、地球が丸いことを示す証拠として『高い山に登ると遠方まで見える』事を取り上げていたこと。もちろん、地球が丸いことは知識としてよく知っていましたし、高い山から見た雄大な風景に感動した経験は何度もありました。
しかしながら、その2つを論理的に地球の形と関連づけて考えたことは一度も無かったのです。
現象と現象を論理で結びつけて、新しい認識に導く科学的思考のおもしろさを教えてくれました。

図１のようにもし地球が平坦であれば、山の高さと関係なく無限の彼方まで見えるはずです。もちろん途中に障害物が話は別ですが、地面が平坦であるとすれば、この推論は『高い山に登るほど遠くまで見える』という体験に反しています。ゆえに、地球は平坦ではないのです。

地球が丸い場合には、図2に示されているような山頂から見ることの出来る範囲（視野の広さは）は、山頂から伸ばした直線と地表面との接点までです。この点を重ねた線が、地平線や水平線です。したがって、地平線や水平線までの距離（L）と山の高さ（ｈ）との関係は、地球の半径をＲ（＝6400㎞）とすると、三平方の定理を使って、次の式を導くことが出来ます。

この式をＬについて解くと

となります。
ところで、地球の半径Rに比べて山の高さhは大変小さいので、上の式は次のように簡単にする事ができます。

そうすれば次のような結果が得られて、『高い山ほど遠くまで見える』事がより実感をもって理解できます。

これに加え、数年前の高校入試勉強会で、東進へ通う高校1年生が話していた言葉が今も忘れられません。
『勉強はつまらないことが多いと思います。僕も高校受験の時を思い返せば、つまらない勉強ばかりしていました。しかし、高校の勉強はとても興味深いものが多いことを分かりました。例えば水の化学式はH2Oですが、HO2ではダメなのかとかを追求していくこと等。高いレベルでの勉強のためにつまらない勉強、つまり基礎勉強は必要であると思います。きっと社会に出たときの仕事もそんなものだと思います。だから、今の受験勉強は決して無駄にはならない、また将来の自分の財産にもなることは間違いないので、本気で勉強してください。将来の自分のためにもお願いします。＜高校受験合格はゴールではなく、新たなスタート＞とはそういうことだと思います。』